In de vorige post hebben we een zogenaamde lasnaadconstructie gepresenteerd. Volgens Hessel betrof het hier een uitzondering op de regel. De regel zoals vastgelegd in de Formule van Euler. Er zou als het ware een ribbe te weinig zijn. Ik heb betoogd dat er onderscheid moet worden gemaakt tussen een ribbe als een meetkundig ding (lasnaad) en als een topologische functie (grens). De lasnaad is één ding met vier grenzen: twee hoekpunten en twee ribben. Zo gesteld is de lasnaadconstructie in overeenstemming met de Formule van Euler.
Hessel presenteerde nog een figuur welke in strijd zou zijn met de Formule van Euler. We noemen dat figuur een laspuntconstructie:
(1)
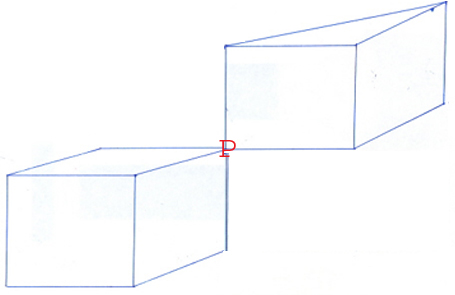
Hesselgewijs zou dit figuur een punt teveel hebben:
(2)

We tonen dit uitgebreider aan in volgend tabel:
(3)
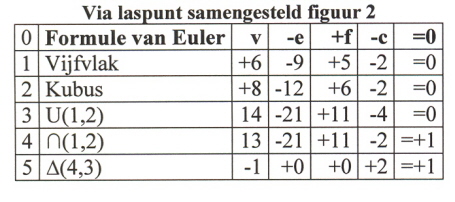
Maar is het inderdaad zo dat er een hoekpunt teveel is?
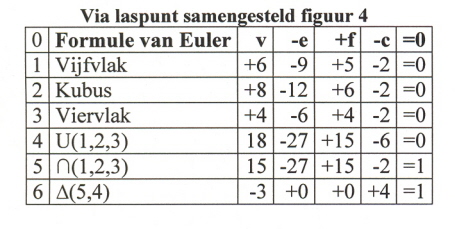
Als we nog eens kijken naar figuur (1) dan zien we dat in punt P drie maal twee ribben elkaar “ontmoetenâ€: twee horizontaal, twee verticaal en twee in de “diepteâ€, waarvan één niet getekend. In wezen betekent dit dat het punt P ingesloten is door zes ribben, zodanig dat er geen ruimte is waar P zichtbaar is. Dat wil zeggen P is niet een grenspunt, dus niet een vertice V. Dus P is ten onrechte meegeteld in tabel (3). Hallo!!! Dus figuur (1) telt niet dertien maar twaalf hoekpunten: v=12. Dus tabel (3) moet worden vervangen door tabel (4) met samengesteld figuur 3:
(4)
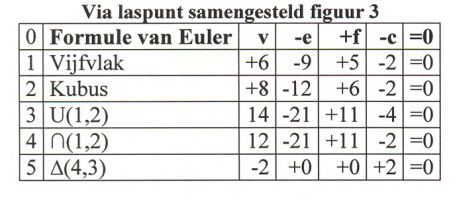
Het lijkt tamelijk bizar dat het enige raakpunt van twee veelvlakken om zo te zeggen onzichtbaar is. Maar het is niet anders dan dat je de toppen van hun neuzen niet ziet wanneer twee Eskimo’s met elkaar neuzen. Dat we gewoon zijn om ingeval van twee veelvlakken die precies één raakpunt met elkaar gemeen hebben dit raakpunt te zien als een grenspunt houdt in dat we iets zien dat er niet is. Anderzijds is het natuurlijk wel zo dat er “ergens†een soort van punt P is. Geen grenspunt, V, maar wat dan wel?
Laten we een willekeurig ander veelvlak raken aan het punt P:
(5)
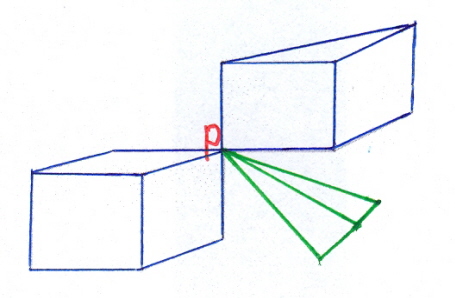
dan impliceert dat:
(6)
We zijn als het ware terug bij af. Blijkens regel 5 lijkt het erop dat met het nieuwe viervlak opnieuw een hoekpunt teveel is geïntroduceerd. Maar nog een hoekpunt eraf halen is niet goed denkbaar.
We voegen aan raakpunt P uit figuur (5) nog een viervlak toe:
(7)
Zoeken we naar constanten in de transformaties van samengesteld figuur 3 via samengesteld figuur 4 naar samengesteld figuur 5 dan kunnen we opmerken:
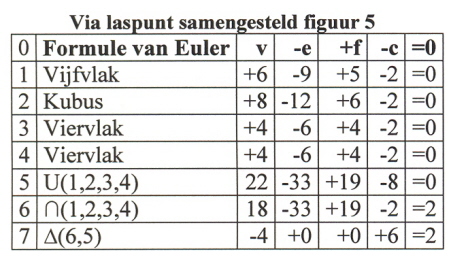
Voor n veelvlakken die elkaar in P ontmoeten geldt, als we telkens de laatste regel van elk tabel bekijken en met elkaar vergelijken, dus regel n+3:
(8)
1) ∆v(n+2,n+1) = -n
Bijvoorbeeld in tabel (4) geldt voor samengesteld figuur 3:
∆v(4,3) = 12 – 14 = -2 = -n
In tabel (6) geldt:
∆v(5,4) = 15 – 18 = -3 = -n
In tabel (7) geldt:
∆v(6,5) = 18 – 22 = -4 = -n
2) ∆-e(n+2,n+1) = ∆-f(n+2,n+1) = 0
3) ∆-c(n+2,n+1) = (n-1)*2
Bijvoorbeeld in tabel (4) geldt voor samengesteld figuur 3:
∆-c(4,3) = -2 –1*-4 = +2 = (n-1)*2; voor n=2
In tabel (6) geldt:
∆-c(5,4) = -2 –1*-6 = +4 = (n-1)*2; voor n=3
In tabel (7) geldt:
∆-c(6,5) = -2 –1*-8 = +6 = (n-1)*2; voor n=4
4) ∆(n+2,n+1) = n-2
‘n-2’ is de waarde rechts van het =teken in de meest rechtse kolom.
Bijvoorbeeld in tabel (4) geldt:
∆(4,3) = 0 = n-2; voor n=2
In tabel (6) geldt:
∆(5,4) = 1 = n-2; voor n=3
In tabel (7) geldt:
∆(6,5) = 2 = n-2; voor n=4
Kortom met elk nieuw veelvlak toegevoegd aan punt P neemt het getal rechts van het =teken met één toe, en verwijdert daarmee zich steeds verder van de door Euler vereiste waarde nul.
In wat algemenere termen gesteld:
(9)

We hebben nu de volgende wat verwarrende situatie:
1) Als we P percipiëren als een grenspunt V dan zien we iets dat er niet is (de neustoppen).
2) P is een ding dat er is en dat we niet zien.
3) Telkens als een nieuw veelvlak raakt aan P dan neemt in de laatste twee regels van de desbtetreffende tabel rechts van het =teken het getal met één toe.
4) Het in 3) genoemde effekt kan niet worden weggepoetst door nog een grenspunt weg te werken. Bijvoorbeeld van een viervlak dat wordt toegevoegd, gaat één punt als het ware op in het punt P, de overige drie hoekpunten blijven gewoon bestaan.
Het is duidelijk dat de Formule van Euler hier geen soelaas biedt. Wat te zeggen van de Formule van Euler-Poincaré?
Deze formule biedt onder meer ingesloten ruimtes en gaten. Wat betreft ingesloten ruimtes, die zijn niet aan de orde. De veelvlakken kunnen zowel hol zijn als massief. En gaten?
Ik stel voor P op te vatten als een gat.
Als we P opvatten als een gat dan kunnen we de Euleriaanse tabel (4) met betrekking tot samengesteld figuur 3 transmuteren naar een een tabel à la de Formule van Euler-Poincaré. We spreken van een gepoincaréseerde tabel.
(10)
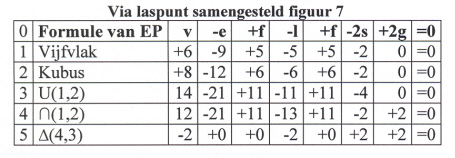
Regel 5 van deze tabel kunnen we als volgt interpreteren. Het zogenoemde raakpunt P is topologisch gesproken niet zozeer een punt als wel een gat. De twee veelvlakken hadden voordat zij elkaar ontmoeten in raakpunt P elk een hoekpunt dat als het ware verdwijnt in in het gat P. Vandaar dat ∆v=-2, ∆l=-2 en ∆2g=2. Bovendien zijn de twee afzonderlijke figuren daarmee opgegaan in één samengesteld figuur, vandaar ∆s=2. We zouden P om te onderscheiden van ‘normale’ gaten een zwart gat kunnen noemen, omdat P als het ware hoekpunten opslokt (telkens als een nieuw toegevoegd veelvlak met één van zijn hoekpunten P raakt, verliest het nieuwe toegevoegde veelvlak zijn desbetreffende hoekpunt) en omdat P onzichtbaar is (P heeft niet een ruimtelijk aanzien zoals een tunnel door een massieve kubus of twee openingen in de wand van een holle kubus).
We kunnen vervolgens naar believen nog een veelvlak aan het raakpunt P toevoegen (zoals getekend in (5)):
(11)
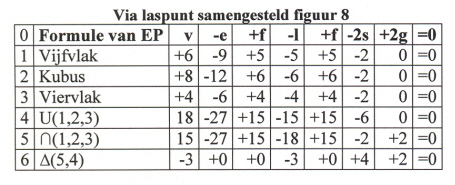
In regel 6 van bovenstaand tabel staat genoteerd welke mutaties er zijn vanaf de logische som van de drie samenstellende figuren naar hun logisch product toe. Dit correspondeert weer met de werking van de operatoren van Euler:
(12) Mgs: g=1
Er is dus één gat gevormd, zoals de waarde in regel 5 van tabel (11) aangeeft.
(13) 3*Mef
(14) 3*Ksfv: s=1, v=15
De aantallen s en v betreffen weer waardes uit regel 5.
(15) 3* KeMl: l=18
Met elk betrokken veelvlak is er één punt verdwenen en één lus toegevoegd.
In algemene termen gesteld, geldt dat telkens als aan het raakpunt P een nieuw veelvlak wordt toegevoegd:
(16) ∆= ∩-U
De mutaties ∆ houden in:
(17) Mfe
(18) Ksfv: één punt en één shell zijn van het toegevoegde veelvlak verdwenen.
(19) KeMl: het in (17) gecreëerde punt P wordt omgezet in een lus.
Per saldo is het alsof met de toevoeging van een nieuw veelvlak aan het raakpunt (gat P) een punt van het toegevoegde veelvlak wordt vernietigd en als herinneringsmonumentje een lus achterlaat (zoals ook elke nieuwe opening in een vlak met de creatie van een lus gepaard gaat).
In de vorige post konden we Euler “redden” voor een bepaalde meetkundige ribbe (ding) in plaats één twee topologische ribben (grenzen) te tellen. In de huidige post kennen we aan een bepaald meetkundig raakpunt P de topologische functie gat toe. Hiermee is Euler niet gered, maar wel is de formule van Euler-Poincaré toegepast.
Dit is de kwintessens van deze post.
