Tot dusverre is gepoogd in kort bestek een idee te geven van de formule van Euler en zijn moderne opvolger, de formule van Euler-Poincaré, zoals deze volgens het boekje worden opgevat. Vanaf nu worden nieuwe ideeën met betrekking tot beide formules geformuleerd. Vergelijk het met de verklanking van de eigen interpretatie van een bestaande compositie door een pianist.
De Duitse delfstofkundige Johann Hessel (1796-1872) heeft in 1832 verschillende meetkundige figuren aangeduid als uitzonderingen op de Eulerformule. Twee ervan zullen we behandelen. Waarvan de eerste in deze post.
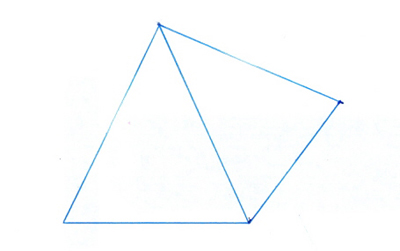
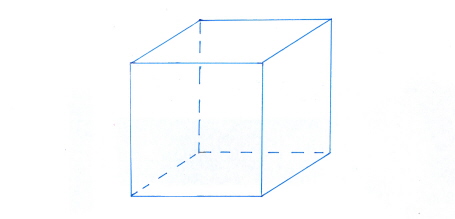
Deze figuur wordt getekend als:
(1)
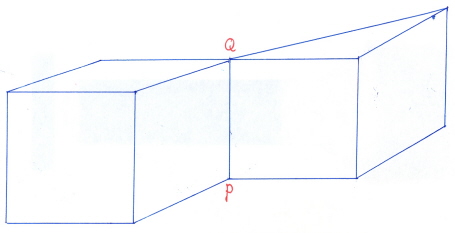
Het gaat hierbij om een vijfvlak en een zesvlak die als het ware aan elkaar zijn gelast.
Tellen we de hoekpunten, ribben en vlakken volgens de formule van Euler dan verkrijgen we volgens Hessel:
(2)
De kneep zit ‘m natuurlijk in de ‘lasnaad’ PQ. Deze wordt door Hessel geteld als één ribbe. Dit kunnen we duidelijker tonen door één en ander uitgebreider weet te geven in de volgende tabel.
(3)
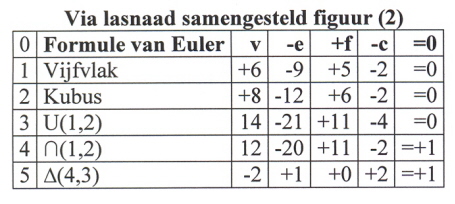
In regel 0 van de tabel hebben we -c geïntroduceerd. Dat wil zeggen de waarde =2 die door Euler rechts van het =teken is geplaatst hebben we naar links van het =teken gebracht en geplaatst onder de noemer –c (constante) uit regel 0.
In regel 3 zijn de waarden van de hoekpunten, ribben, vlakken en constanten met betrekking tot het vijfvlak en de kubus eenvoudigweg bij elkaar opgeteld. Dus de waarden uit regel 1 en 2 zijn bij elkaar opgeteld. Rechts van het =teken staat keurig netjes de waarde nul.
Als we nu de waarden uit regel 2 en 3 bij elkaar voegen zoals Hessel dat bedoelde dan verkrijgen we regel 4. Rechts van het =teken staat +1 in plaats van 0. In regel 5 staat beschreven wat er eigenlijk is gebeurd van regel 3 naar regel 4. De waarde van de hoekpunten is per saldo van regel 3 naar regel 4 met 2 gedaald. Dit kan worden weggestreept tegen het gegeven dat de constante van de samengevoegde veelvlakken niet –4 (regel 3) maar –2 (regel 4) is, dus met 2 gestegen. Blijft over het gegeven dat volgens Hessel de totale waarde van de ribben met één is gestegen. Dat wil zeggen ribbe PQ telt in de samenvoeging voor 1, terwijl deze als som van beide veelvlakken in regel 3 als 1+1=2 gold. Dus van twee ribbes PQ van de afzonderlijke veelvlakken naar één ribbe PQ in de samengestelde figuur.
Meetkundig is het inderdaad zo dat de samenvoeging van beide veelvlakken tot één negenvlak ertoe leidt dat uit twee ribbes PQ (één uit elk van beide samenstellende figuren) er één ribbe PQ bij wijze van lasnaad ontstaat. Nogmaals, meetkundig is dat zo. Evenwel niet topologisch. Topologisch is een ribbe niet een ding (zoals bijvoorbeeld een ijzeren staaf), maar een functie. Dat wil zeggen een grensfunctie van een ding. Het ‘ding’ PQ in de samengestelde figuur heeft vier grensfuncties. Aan beide uiteinden een hoekpunt, v. En aan ‘voorkant’ en de ‘achterkant’ van de samengestelde figuur een ribbe, met waarde e. Dat wil zeggen de samengestelde figuur heeft langs de lasnaad PQ niet één, maar twee functionele ribben, edges.
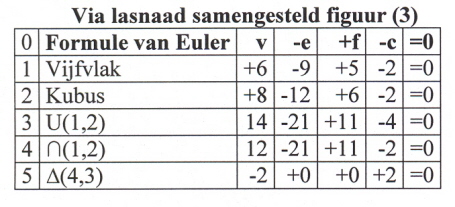
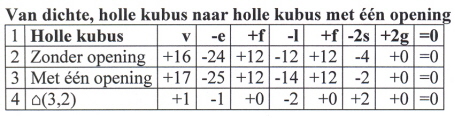
Tabel 3 is dus in principe onjuist en dient te worden vervangen door tabel 4:
(4)
Logische som en logisch product
In tabel 3 en in tabel 4 zien we op de regels 3, 4 en 5 de volgende symbolen staan. Het U-symbool voor de logische som, het omgekeerde teken daarvan voor het logisch produkt (∩) en op regel 5 het wiskundige symbool voor verandering, ∆.
Een samengesteld figuur impliceert een context waarbinnen beide samenstellende delen (kubus en vijfvlak) op één of andere manier voorkomen. Dit is een inperking van hun logische som: het logisch product.
De logische som van –bijvoorbeeld- stukken hout en glas is een opsomming van de afzonderlijke elementen. Deze afzonderlijke elementen behoeven niet samen binnen één en dezelfde context voor te komen om een logische som te vormen. Een huis is een logische product van dergelijke elementen. Binnen het geheel dat een huis is worden de samenstellende elementen op een bepaalde en niet op een andere wijze gebruikt. De samenstellende delen vormen daarentegen een logisch product indien ze binnen één en dezelfde context voorkomen. Het geheel (huis of bijvoorbeeld het samengestelde negenvlak) is daarmee niet groter (zoals zo vaak gesteld), maar juist kleiner dan de som der (afzonderlijke) delen. De som geeft het potentieel van het gebruik, het geheel van de mogelijke contexten waarbinnen ze kunnen voorkomen, aan en het product geeft het gerealiseerde gebruik, één geactualiseerde context, aan.
Met het ∆-teken wordt het verschil tussen het product en de logische som uitgedrukt van de samenstellende figuren kubus en vijfvlak. Als de formule van Euler klopt dan geldt dat in al de drie gevallen, U(1,2), ∩(1,2) en ∆(4,3) rechts van het =teken de waarde 0 staat.
Blijkens tabel 4 is dat zo.
Het onderscheid tussen logische som en logisch product wordt in zogenaamde waarheidstafels tot uitdrukking gebracht. In een logische som behoeven de samenstellende delen A en B niet per se in dezelfde context te fungeren.
(5)
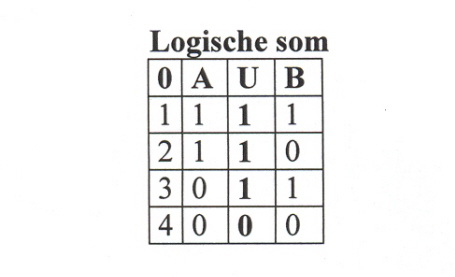
Bij een logisch product wel.
(6)
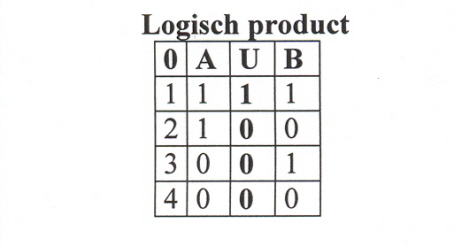
Merk op dat bij een logische som de waarden A en B inderdaad worden opgeteld (bijvoorbeeld regel 2 in tabel 5: 1 + 0 =1) en bij een logisch product de logische waarden inderdaad met elkaar worden vermenigvuldigd (bijvoorbeeld regel 2 in tabel 6: 1 * 0 =0).
De waarde 1 betekent waar en de waarde 0 betekent onwaar. De uiteindelijke logische waarde van een logische uitspraak (bijvoorbeeld A U B) staat per regel onder het symbool U (tabel 5)of het ∩ (tabel 6)aangegeven.
Referentie
de in deze post geanalyseerde lasnaadcontrsuctie wordt, zoals hierboven geschreven, in de vaklitterauur beschouwd als een typisch voorbeeld van een uitzonder op de Formule van Euler. Ik baseer me hierbij op het heel fraaie en waardevolle boek van David S. Richeson Euler’s Gem. In de komende posts zal de nodige informatie worden geput uit dit boek.
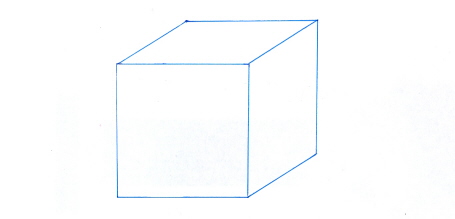
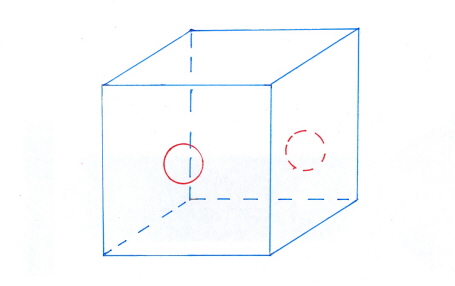
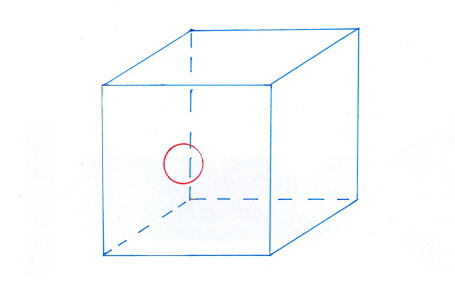De opening is een ‘rondje’ dat bestaat uit één hoekpunt en één ribbe; zowel aan de ‘binnenkant’ als aan de ‘buitenkant’ van de wand van de holle kubus is er een lus of loop (l) om de opening heen. De opening heeft dus twee lussen. De opening bestaat evenwel uit slechts één ribbe (e) en één hoekpunt (v).
