In de vorige post hebben we de Kleine Stervormige Dodecaëder (KSD) behandeld. Hoewel deze door een grootheid als Schläfli is beschouwd als een uitzondering op de regel van Euler kan ze wel degelijk in termen van de formule van Euler-Poincaré worden gegoten. De KSD kan zelfs, als we het geheel als compact opvatten, in termen van de formule van Euler worden beschreven (zie het Besluit van de vorige post).
In de huidige post beschouwen we de de Grote Dodecaëder, welke om overeenkomstige redenen als de Kleine Stervormige Dodecaëder, door verschillende auteurs is beschreven als uitzondering op de formule van Euler.

Grote Dodecaëder

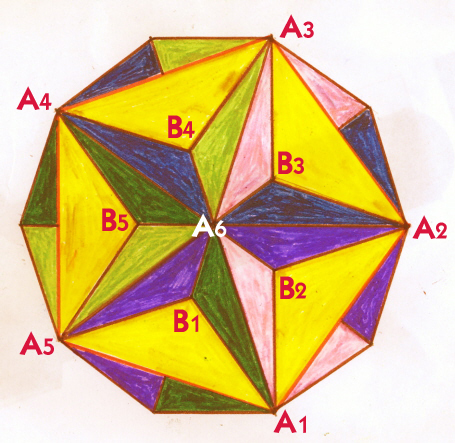
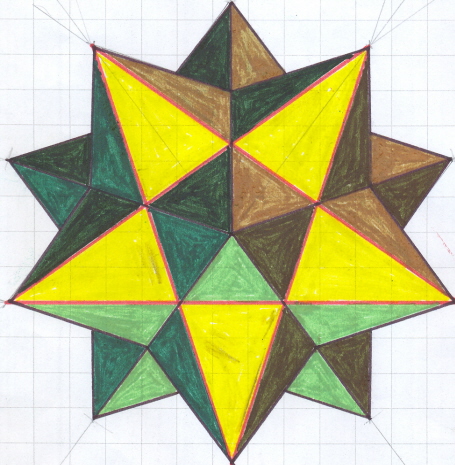
Afbeelding (1):
de Grote Dodecaëder
Ontleend aan oorpronkelijk ontwerp en concept van Tom Ruen; SVG-creatie Júlio Reis

De Grote Dodecaëder is ingewikkelder dan de Kleine Stervormige. Geen drie, maar vier niveaus. Te weten:

De buitenkant toont zich als een eenaanschakeling van twintig driekantige puntzakken. Bijvoorbeeld A1A2A6B2, waarbij B2 het diepstgelegen punt is (zie afbeelding (1).
Dus de buitenkant is een skelet van een regelmatige twintigvlak, met dienverstande dat in plaats van twintig vlakken er zestig vlakken zijn:

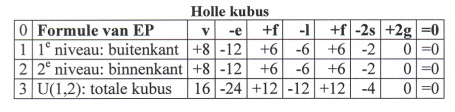
v – e + f = (12+20) – (30 + 20*3) + (20*3)

Het geraamte van de icosaëder (regelmatig twintigvlak) aan de buitenkant impliceert dat er dertig ribben zijn (die als het ware de puntzakken begrenzen). Aan elk zo’n ribbe grenzen twee vlakken, elk vlak daarvan ligt in een puntzak. Omgekeerd grenst elk zo’n vlak aan precies één ribbe van de icosaëder. Bijvoorbeeld de vlakken A1B1A6 en A1B2A6 grenzen aan de ribbe A1A6.
Dat wil zeggen aan keerzijde van alle (zestig) vlakken van de buitenkant zijn telkens per ribbe van de dodecaëder twee vlakken van het tweede niveau. Afbeelding (1) laat zien dat elk zo’n tweetal vlakken tesamen met een tweetal andere vlakken van het tweede niveau welke niet de keerzijde zijn van een (deel)vlak van het eerste niveau een viervlak vormen. Bijvoorbeeld het viervlak A1B1A6 B2 bestaat uit de vlakken A1B1A6 en A1B2A6 aan de keerzijde van vlakken van het eerste niveau en de vlakken A1B1B2 en B1B2A6 aan de keerzijde van vlakken van het derde niveau.
Omdat er dertig van zulke ribben als A1A6 zijn, zien we dertig viervlakken die met elkaar het tweede niveau vormen. Dat wil zeggen:

v – e + f = (30*4) – (30*6) + (30*4)

Op afbeelding (1) is te zien dat vijf viervlakken van het tweede niveau “staan” op de gele vijfhoek A1A2A3A4A5. De vijf viervlakken begrenzen met de gele vijfhoek een piramide met grondvlak B1B2B3B4B5 en top A6. Er zijn twaalf vlakken zoals A1A2A3A4A5, dat wil zeggen er zijn twaalf van die piramiden met één grondvlak en vijf opstaande zijden (de opstaande vlakken: B1B2A6, B2B3A6, B3B4A6, B4B5A6 en B5B1A6). Dus voor het derde niveau geldt:

v – e + f = (12*6) – (12*10) + (12*6)

De twaalf piramiden van het derde niveau staan elk op een grondvlak, welke aan de keerzijde (op het vierde niveau) een vlak heeft dat deel uit maakt een regelmatig twaalfvlak. B1B2B3B4B5 is één van die twaalf vlakken. Dat wil zeggen voor het vierde niveau geldt:

v – e + f = 20 – 30 + 12

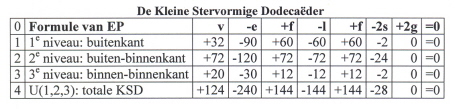
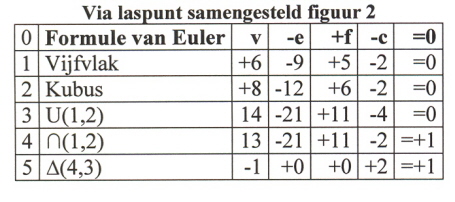
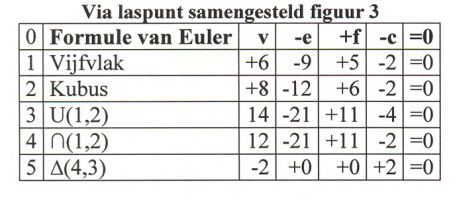
Samengevat in tabel (2):

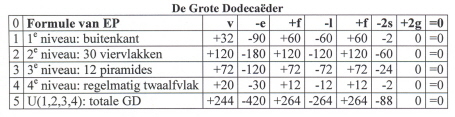
De Grote Dodecaëder is evenals de Kleine Stervormige Dodecaëder een figuur dat door twaalf vijfhoekige vlakken die elkaar doorsnijden te beschrijven als een geheel van holtes. Zou zo’n hol object worden “volgegooid” met zand of zo dan voldeed het aan de formule van Euler (beschrijving op het eerste niveau, de buitenkant).
Evenals in het geval van de KSD telde Schläfli bij de GD twaalf vlakken. In zekere zin is dat ook zo. Maar als er geteld wordt volgens de regels van de formule van Euler-Poincaré dan zijn het er heel wat meer. In totaal maar liefst 264 vlakken. De term vlak kan dus uiteenlopende betekenissen hebben. Als het gaat om een ding met gaten en/of holtes dan is het raadzaam om de betekenis van Euler-Poincaré te hanteren.

Besluit
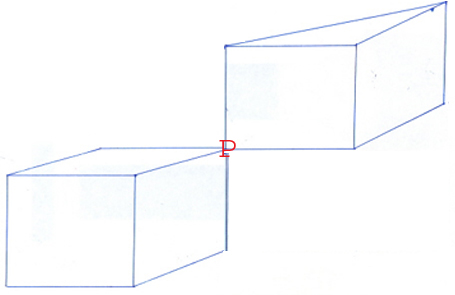
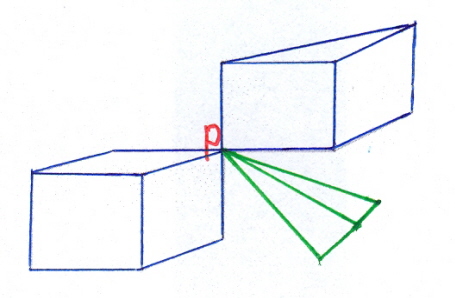
De laatste vier posts (inclusief deze) onderzoeken telkens de in populair wetenschappelijke literatuur(Richeson: hij verdient een eervolle vermelding voor zijn voorbeeldige popularisering van de topologie) en vakliteratuur (Wolfram, Schläfli, Coxeter, Poinsot) weergeven opvatting dat een bepaald figuur (zie met name lasnaadconstructie, laspuntconstructie, Kleine Stervormige Dodecaëder, Grote Dodecaëder) niet in overeenstemming is met de formule van Euler. Alleen van de lasnaadconstructie kan worden gesteld dat ze wel degelijk in overeenstemming is met de formule van Euler. De overige drie zijn heel wel in overstemming met de formule van Euler-Poincaré. De laatste twee betreffen holtes die beschreven worden in termen van de EPF en de laspuntconstructie betreft een centraal gat dat kan worden weergegeven in de EPF. De formule van Euler (EF) is in dergelijke gevallen ontoereikend. Hoogstens in grensgevallen van betekenis. Bijvoorbeeld als de KSD compact is.

In de volgende posts komen ideeën aan bod die zover ik weet (deels) nieuw zijn. Het draait allemaal om het thema “het pi-gehalte van diverse meetkundige objecten”. Kortweg: hoeveel graden bedragen objecten zoals bijvoorbeeld kubus, bol, vierkant of schijf?

De twee voorafgaande posts, Lasnaadconstructie en Laspuntconstructie betroffen (al dan niet vermeende) uitzonderingen op de formule van Euler, welke door Hessel in 1832 zijn beschreven. Eerder nog in 1810 heeft Louis Poinsot twee uitzonderingen beschreven. Later duiken die twee uitzonderingen weer op in een boek van Schläfli. Wij knopen daarop aan.
In deze post worden zaken opnieuw uit de doeken gedaan die al eerder behandeld zijn. Zoals de formule van Euler en de formule van Euler-Poincaré. Enerzijds komt het doordat dit verhaal (wat u nu leest) al eens door mij is opgeschreven voordat ik wist dat deze weblog ooit zou verschijnen. Anderzijds heb ik dat zo gelaten omdat het verhaal zo beter is te volgen.

Op de webpagin’s van Wolfram met betrekking tot de Kleine Stervormige Dodecaëder en de Grote Dodecaëder wordt er op gewezen dat Schläfli de desbetreffende dodecaëder niet erkent als een regelmatig driedimensionaal lichaam.
Ik citeer:

Schläfli (1901, p. 134) did not recognize the small stellated dodecahedron [c.q. the great dodecahedron] as a regular solid because it violates the polyhedral formula, instead satisfying
N0 – N1 + N2 = 12 – 30 + 12 = -6
where N0 is the number of vertices, N1 the number of edges, and N2 the number of faces (Coxeter 1973, p. 172).

De “polyhedral formula” is de formule van Euler (gepubliceerd in 1752), welke ook wel wordt genoteerd als:

(1) V – E + F = 2
(V is het aantal vertices, E is het aantal edges en F is het aantal faces van een veelvlak).

De formule van Euler heeft in principe betrekking op lichamen zonder gaten. Later heeft Lhuilier in 1865 de formule uitgebreid voor de gevallen dat er gaten in het spel zijn:

(2) V – E + F = 2 – 2g
G betreft het aantal gaps.

Weer later heeft Poincaré (gepubliceerd in 1895) een formule gegeven waarin ook rekening wordt gehouden met holtes binnen een lichaam. Een holte is een ruimte, omsloten door vlakken: een afgesloten binnenruimte.
Deze formule beschrijven we in de volgende paragraaf.
Opgemerkt kan worden dat dodecaëders (Grote, Kleine Stervormige of de platonische) doorgaans geen gaten bevatten.
Wel zij vastgesteld dat zowel de Kleine Stervormige (KSD) als de Grote Dodecaëder (GD) tengevolge van doorsnijdingen van de vlakken holtes bevatten.
Hieruit volgt:

In de volgende paragraaf formuleren we de formule van Euler-Poincaré (deze is de door Poincaré uitgebreide formule van Euler).

De formule van Euler-Poincaré

Op een webpagina van het MIT wordt de formule van Euler-Poincaré beschreven en met voorbeelden toegelicht.

De formule luidt als volgt:

(3) V – E + F – (L-F) – 2(S – G) = 0

Een aantal symbolen kwamen we al eerder tegen:
V = aantal hoekpunten, E = aantal ribben, F = aantal vlakken en G = aantal gaten. In onze beschouwing gaan we uit van G = 0.
Nieuw zijn de symbolen L en S.
L staat voor aantal loops (lussen). Met elk vlak correspondeert altijd één outer loop. Als een vlak ontbreekt of onderbroken wordt dan correspondeert daarmee een inner loop. L is dan groter dan F. Op de pagina van het MIT worden voorbeelden van inner loops gegeven. Wij gaan hier niet op in, voor ons zijn deze niet van belang: dat wil zeggen voor de dodecaëders zoals hier behandeld geldt L=F.
S staat voor aantal shells. Een compact lichaam heeft altijd één schil; S=1. Een doos heeft twee schillen: S=2. De buitenkant van de doos heeft namelijk één schil, de holle binnenkant impliceert nog één schil. Dus buiten- plus binnenkant zijn twee schillen.

Een eenvoudige toepassing van de formule van Euler-Poincaré betreft een compacte kubus:

(4) v=8, e=12, f=6, l=6, g=0:
v-e+f-(l-f)-2(s-g)=8-12+6-(6-6)-2(1-0)=0

Is een kubus niet compact, maar hol:

(5)

Aan de keerzijde van elk vlak van het eerste niveau is er een vlak van het tweede niveau.

Een analoog voorbeeld is dat van een regelmatig twaalfvlak met holle binnenkant:

(6)

In de volgende paragraaf passen we formule van Euler-Poincaré toe op de Kleine Stervormige Dodecaëder.

De Kleine Stervormige Dodecaëder

Afbeelding (7):
de Kleine Stervormige Dodecaëder
Ontleend aan oorpronkelijk ontwerp en concept van Tom Ruen; SVG-creatie Júlio Reis

Figuur (7) zullen we in eerste instantie beschrijven à la Schläfli:

(8)

Alles wat van dezelfde kleur is, representeert één van de twaalf vlakken die elkaar doorsnijden. Dus de driehoekige vlakken die door opdeling tengevolge van de doorsnijdingen van twaalf vijfvijfhoekige vlakken er zijn worden om zo te zeggen niet in rekening gebracht. Zo ook worden de ribben en hoekpunten die deel uitmaken van de driehoeken niet meegeteld. Alleen de ribben en hoekpunten die deel uitmaken van de twaalf vijfhoeken worden geteld. Vandaar tabel (8).

Als we de figuur beschrijven in termen van de formule van Euler-Poincaré, dat wil zeggen we houden rekening met holtes tengevolge van de vlakken die elkaar doorsnijden, dan komen we tot het volgende.

De Kleine Stervormige Dodecaëder omvat drie niveaus. Te weten:

Aan de buitenkant toont de KSD zich als een geheel van twaalf aaneengeschakelde vijfkantige torenspitsen, die congruent zijn. In het midden van afbeelding (7) zien we zo’n vijfkantige torenspits.
Zou elke torenspits vervangen worden door een vlak dan toonde de “getransformeerde” KSD zich aan de buitenkant als een regelmatige twaalfvlak, een platonische dodecaëder. Dat wil zeggen twintig hoekpunten, dertig ribben en twaalf vlakken. (a)
Evenwel in de KSD is elk van de zojuist genoemde twaalf vlakken in werkelijkheid een torenspits, bestaande uit vijf opstaande vlakken, vijf opstaande ribben en één hoekpunt, de spits. Dus dragen de twaalf torenspitsen tesamen bij: twaalf hoekpunten, zestig ribben en zestig vlakken. (b)
(a) + (b): v – e + f = (20+12) – (30+60) + (0+60).
De buitenkant heeft per definitie één schil: s=1, dus -2s=-2

Elk zo’n binnenkant is een piramide met een vijfhoekig grondvlak. Dus per binnenpiramide: zes hoekpunten, tien ribben en zes vlakken. Er zijn twaalf van zulke piramiden. Dus in totaal: v – e + f = 72 – 120 + 72.
Er zijn twaalf holle piramides, dus: s=12, -2s=-24.

Aan de keerzijde van elk grondvlak van een piramide uit het tweede niveau is een zijvlak van één binnendodecaëder (een regelmatige twaalfvlak in het binnenste van de KSD). Dus voor het derde niveau geldt:
v – e + f -2s = 20 – 30 + 12 – 2.

Samengevat in (9):

In totaal zijn er veertien schillen, waarvan dertien een holte betreffen.

Besluit
1) Zou de beschrijving zoals in tabel (9) zicht beperken tot het eerste niveau dan was de figuur beschreven als een compact ding; dat zo beschreven ook in overeenstemming is met de formule van Euler.
2) Zou het derde niveau compact (en de piramides van het tweede niveau hol) zijn dan waren er geen veertien, maar dertien schillen.
3) De beschrijving à la Schläfli is een interpretatie van de formule van Euler. De formule van Euler is, hoe deze ook wordt geïnterpreteerd, niet geschikt om een figuur met holtes te beschrijven. En zoals we in de eerste slotopmerking schreven: als de figuur wordt opgevat als een compact ding dan kan ze wel degelijk in termen van Euler worden beschreven. Wordt het opgevat als een hol ding dan kan het alleen adequaat worden beschreven in termen van Euler-Poincaré.

In de vorige post hebben we een zogenaamde lasnaadconstructie gepresenteerd. Volgens Hessel betrof het hier een uitzondering op de regel. De regel zoals vastgelegd in de Formule van Euler. Er zou als het ware een ribbe te weinig zijn. Ik heb betoogd dat er onderscheid moet worden gemaakt tussen een ribbe als een meetkundig ding (lasnaad) en als een topologische functie (grens). De lasnaad is één ding met vier grenzen: twee hoekpunten en twee ribben. Zo gesteld is de lasnaadconstructie in overeenstemming met de Formule van Euler.
Hessel presenteerde nog een figuur welke in strijd zou zijn met de Formule van Euler. We noemen dat figuur een laspuntconstructie:

(1)

Hesselgewijs zou dit figuur een punt teveel hebben:

(2)

We tonen dit uitgebreider aan in volgend tabel:

(3)

Maar is het inderdaad zo dat er een hoekpunt teveel is?
Als we nog eens kijken naar figuur (1) dan zien we dat in punt P drie maal twee ribben elkaar “ontmoeten”: twee horizontaal, twee verticaal en twee in de “diepte”, waarvan één niet getekend. In wezen betekent dit dat het punt P ingesloten is door zes ribben, zodanig dat er geen ruimte is waar P zichtbaar is. Dat wil zeggen P is niet een grenspunt, dus niet een vertice V. Dus P is ten onrechte meegeteld in tabel (3). Hallo!!! Dus figuur (1) telt niet dertien maar twaalf hoekpunten: v=12. Dus tabel (3) moet worden vervangen door tabel (4) met samengesteld figuur 3:

(4)

Het lijkt tamelijk bizar dat het enige raakpunt van twee veelvlakken om zo te zeggen onzichtbaar is. Maar het is niet anders dan dat je de toppen van hun neuzen niet ziet wanneer twee Eskimo’s met elkaar neuzen. Dat we gewoon zijn om ingeval van twee veelvlakken die precies één raakpunt met elkaar gemeen hebben dit raakpunt te zien als een grenspunt houdt in dat we iets zien dat er niet is. Anderzijds is het natuurlijk wel zo dat er “ergens” een soort van punt P is. Geen grenspunt, V, maar wat dan wel?

Laten we een willekeurig ander veelvlak raken aan het punt P:

(5)

dan impliceert dat:

(6)

We zijn als het ware terug bij af. Blijkens regel 5 lijkt het erop dat met het nieuwe viervlak opnieuw een hoekpunt teveel is geïntroduceerd. Maar nog een hoekpunt eraf halen is niet goed denkbaar.

We voegen aan raakpunt P uit figuur (5) nog een viervlak toe:

(7)

Zoeken we naar constanten in de transformaties van samengesteld figuur 3 via samengesteld figuur 4 naar samengesteld figuur 5 dan kunnen we opmerken:
Voor n veelvlakken die elkaar in P ontmoeten geldt, als we telkens de laatste regel van elk tabel bekijken en met elkaar vergelijken, dus regel n+3:

(8)

1) ∆v(n+2,n+1) = -n

Bijvoorbeeld in tabel (4) geldt voor samengesteld figuur 3:
∆v(4,3) = 12 – 14 = -2 = -n

In tabel (6) geldt:
∆v(5,4) = 15 – 18 = -3 = -n

In tabel (7) geldt:
∆v(6,5) = 18 – 22 = -4 = -n

2) ∆-e(n+2,n+1) = ∆-f(n+2,n+1) = 0

3) ∆-c(n+2,n+1) = (n-1)*2

Bijvoorbeeld in tabel (4) geldt voor samengesteld figuur 3:
∆-c(4,3) = -2 –1*-4 = +2 = (n-1)*2; voor n=2

In tabel (6) geldt:
∆-c(5,4) = -2 –1*-6 = +4 = (n-1)*2; voor n=3

In tabel (7) geldt:
∆-c(6,5) = -2 –1*-8 = +6 = (n-1)*2; voor n=4

4) ∆(n+2,n+1) = n-2
‘n-2’ is de waarde rechts van het =teken in de meest rechtse kolom.

Bijvoorbeeld in tabel (4) geldt:
∆(4,3) = 0 = n-2; voor n=2

In tabel (6) geldt:
∆(5,4) = 1 = n-2; voor n=3

In tabel (7) geldt:
∆(6,5) = 2 = n-2; voor n=4

Kortom met elk nieuw veelvlak toegevoegd aan punt P neemt het getal rechts van het =teken met één toe, en verwijdert daarmee zich steeds verder van de door Euler vereiste waarde nul.

In wat algemenere termen gesteld:
(9)

We hebben nu de volgende wat verwarrende situatie:
1) Als we P percipiëren als een grenspunt V dan zien we iets dat er niet is (de neustoppen).
2) P is een ding dat er is en dat we niet zien.
3) Telkens als een nieuw veelvlak raakt aan P dan neemt in de laatste twee regels van de desbtetreffende tabel rechts van het =teken het getal met één toe.
4) Het in 3) genoemde effekt kan niet worden weggepoetst door nog een grenspunt weg te werken. Bijvoorbeeld van een viervlak dat wordt toegevoegd, gaat één punt als het ware op in het punt P, de overige drie hoekpunten blijven gewoon bestaan.

Het is duidelijk dat de Formule van Euler hier geen soelaas biedt. Wat te zeggen van de Formule van Euler-Poincaré?
Deze formule biedt onder meer ingesloten ruimtes en gaten. Wat betreft ingesloten ruimtes, die zijn niet aan de orde. De veelvlakken kunnen zowel hol zijn als massief. En gaten?
Ik stel voor P op te vatten als een gat.
Als we P opvatten als een gat dan kunnen we de Euleriaanse tabel (4) met betrekking tot samengesteld figuur 3 transmuteren naar een een tabel à la de Formule van Euler-Poincaré. We spreken van een gepoincaréseerde tabel.

(10)

Regel 5 van deze tabel kunnen we als volgt interpreteren. Het zogenoemde raakpunt P is topologisch gesproken niet zozeer een punt als wel een gat. De twee veelvlakken hadden voordat zij elkaar ontmoeten in raakpunt P elk een hoekpunt dat als het ware verdwijnt in in het gat P. Vandaar dat ∆v=-2, ∆l=-2 en ∆2g=2. Bovendien zijn de twee afzonderlijke figuren daarmee opgegaan in één samengesteld figuur, vandaar ∆s=2. We zouden P om te onderscheiden van ‘normale’ gaten een zwart gat kunnen noemen, omdat P als het ware hoekpunten opslokt (telkens als een nieuw toegevoegd veelvlak met één van zijn hoekpunten P raakt, verliest het nieuwe toegevoegde veelvlak zijn desbetreffende hoekpunt) en omdat P onzichtbaar is (P heeft niet een ruimtelijk aanzien zoals een tunnel door een massieve kubus of twee openingen in de wand van een holle kubus).

We kunnen vervolgens naar believen nog een veelvlak aan het raakpunt P toevoegen (zoals getekend in (5)):
(11)

In regel 6 van bovenstaand tabel staat genoteerd welke mutaties er zijn vanaf de logische som van de drie samenstellende figuren naar hun logisch product toe. Dit correspondeert weer met de werking van de operatoren van Euler:

(12) Mgs: g=1
Er is dus één gat gevormd, zoals de waarde in regel 5 van tabel (11) aangeeft.

(13) 3*Mef

(14) 3*Ksfv: s=1, v=15
De aantallen s en v betreffen weer waardes uit regel 5.

(15) 3* KeMl: l=18
Met elk betrokken veelvlak is er één punt verdwenen en één lus toegevoegd.

In algemene termen gesteld, geldt dat telkens als aan het raakpunt P een nieuw veelvlak wordt toegevoegd:

(16) ∆= ∩-U

De mutaties ∆ houden in:

(17) Mfe

(18) Ksfv: één punt en één shell zijn van het toegevoegde veelvlak verdwenen.

(19) KeMl: het in (17) gecreëerde punt P wordt omgezet in een lus.

Per saldo is het alsof met de toevoeging van een nieuw veelvlak aan het raakpunt (gat P) een punt van het toegevoegde veelvlak wordt vernietigd en als herinneringsmonumentje een lus achterlaat (zoals ook elke nieuwe opening in een vlak met de creatie van een lus gepaard gaat).

In de vorige post konden we Euler “redden” voor een bepaalde meetkundige ribbe (ding) in plaats één twee topologische ribben (grenzen) te tellen. In de huidige post kennen we aan een bepaald meetkundig raakpunt P de topologische functie gat toe. Hiermee is Euler niet gered, maar wel is de formule van Euler-Poincaré toegepast.
Dit is de kwintessens van deze post.